There’s a Bigger Difference Between 6 and 10 Than You Think
Looking for news you can trust?Subscribe to our free newsletters.
What the hell?
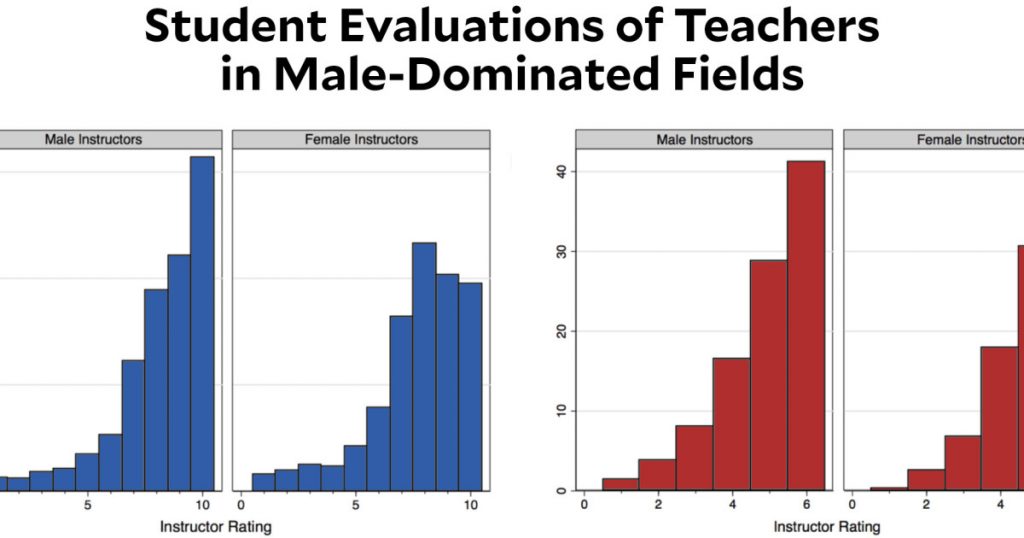
This is exactly what it looks like. A large research university decided to switch its teaching evaluation surveys from a 10-point scale to a 6-point scale. In most fields, this made little difference. But in fields that are traditionally male-dominated, the enormous gender gap in evaluations disappeared. Why?
This chart comes from a new paper by Lauren Rivera and András Tilcsik, and they don’t really seem to know either. Here’s what they say:
Drawing from a complementary survey experiment, we show that this effect is not due to gender differences in instructor quality. Rather, it is driven by differences in the cultural meanings and stereotypes raters attach to specific numeric scales. Whereas the top score on a 10-point scale elicited images of exceptional or perfect performance—and, as a result, activated gender stereotypes of brilliance manifest in raters’ hesitation to assign women top scores—the top score on the 6-point scale did not carry such strong performance expectations. Under the 6-point system, evaluators recognized a wider variety of performances—and, critically, performers—as meriting top marks. Consequently, our results show that the structure of rating systems can shape the evaluation of women’s and men’s relative performance and alter the magnitude of gender inequalities in organizations.
In other words, students viewed a 9 or 10 on a scale of 1-10 as implying true brilliance, and they were reluctant to evaluate female instructors as brilliant. However, a 6 on a scale of 1-6 doesn’t carry the same connotations. Students interpret it as really good, but not necessarily brilliant. Because of that, they were perfectly happy to evaluate the top female instructors with the top evaluation.
Do you believe this? Do I believe it? Beats me. The sample size in the study is large, so that’s not a problem. The switch to a 6-point scale was unrelated to gender concerns, so that’s not an issue. The modeling appears to be reasonable. And the change in results is large. The effect sure seems real, but it’s still anyone’s guess about why the effect is real and why it’s so large. Given my respect for cognitive biases like framing effects, the authors’ explanation seems OK to me, but it’s still a bit of a guess. I’d sure like to hear a few other people weigh in.