How to Draw an Elephant Using Trigonometry
Looking for news you can trust?Subscribe to our free newsletters.
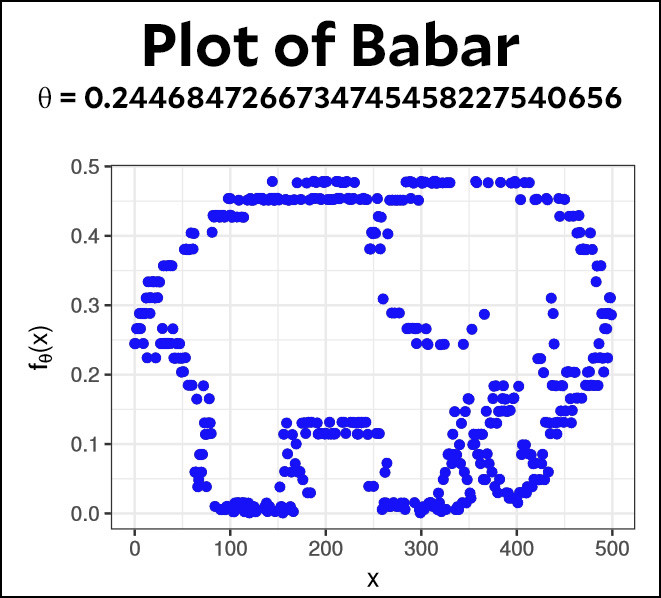
Alex Tabarrok points to a new paper this morning that should thrill data nerds and chart enthusiasts everywhere. Steven Piantadosi of the University of Rochester has produced a simple equation with one variable that is “not novel mathematically” but can perfectly fit any set of scatterplot points. Here it is:
As long as you pick your value of θ with extreme precision, this equation will provide a fit of any data, no matter how complex. Piantadosi demonstrates how this works by fitting a scatterplot of an elephant:
How about that? Give me any set of points, and I can describe them precisely with a universal, single-valued equation. All I have to do is choose θ really, really carefully.
As it happens, this is more a novelty than anything else, but Piantadosi says it contains a warning for artificial intelligence:
The existence of this model has implications for statistical model comparison, and shows that great care must be taken in machine learning efforts to discover equations from data since some simple models can fit any data set arbitrarily well.
A human mathematician is unlikely to be fooled by this, but a machine-learning algorithm could easily decide that the best fit for a bunch of data is an equation like the one above. After all, it works, doesn’t it?